Grid Surfaces

A grid surface is an alternative to a regular triangle-based surface for representing objects with a surface area. Rather than triangular facets, a grid surface is constructed from a grid of quadrilateral points called cells.

Unlike a Surface , a GridSurface cannot contain holes and cannot have any disconnected components. This restricts what a GridSurface can represent; however, they are more compact and simpler, which can make it easier to avoid defects.

The points in a GridSurface are arranged into a grid with GridSurface.major_dimension_count rows and GridSurface.minor_dimension_count columns. When creating and editing a GridSurface, you should be careful to ensure that the points are within the grid.

GridSurface properties

The following is a list of properties and methods that are specific to GridSurface :

Name	Description
cell_points	Use this property to set and access the cell points of a GridSurface . There is a subtle difference between the properties points and cell_points. Cell points are the points rearranged into the underlying grid structure. This allows for points to be referred to via row and column rather than by index. To return the point in the specified row and column, use the notation `cell_points[row, column]`.
cell_point_colours	Use this property to set the colour for each cell point in a `GridSurface`. Note the distinction between a point and a cell point (see above).
cell_visibility_2d	Use this property to set the visibility for a cell to either `True` or `False`. Unlike the `cell_visibility` property, this allows you to select cells via row and column rather than index.
cell_point_selection	Use this property to set the selection for each cell point to either `True` or `False`.
cell_point_visibility	Use this property to set the visibility for each cell point to either `True` or `False`.

Grid surface examples

Constructing a grid surface

The GridSurface constructor requires the following arguments:

major_dimension_count: The number of points in each major dimension of the grid
minor_dimension_count: The number of points in each minor dimension of the grid

The major and minor dimension counts determine the size of the grid. Given a major dimension count of X and a minor dimension count of Y, the grid surface will contain an X ✕ Y grid of points defining a (X - 1) ✕ (Y - 1) grid of cells. Once you have created a GridSurface object, you cannot change its major and minor dimension counts. This means that its point and cell counts will remain the same.

You can pass the following additional optional arguments to a GridSurface constructor:

x_step: The distance between adjacent points in the x direction of the grid surface.
y_step: The distance between adjacent points in the y direction of the grid surface.
start: The start point to generate the grid of points. The default is the origin ([0, 0, 0]).
column_major: A boolean value indicating whether the grid is a column major or row major.

If column_major is set to True (column major), the x corresponds to columns and y corresponds to rows. If column_major is set to False, the x corresponds to rows and y corresponds to columns. If you omit this property from the constructor, it will automatically be set to false, indicating a row major grid.

Passing the x_step, y_step and start parameters to the GridSurface constructor populates the x and y coordinates of the points of a regular grid with the specified step values.

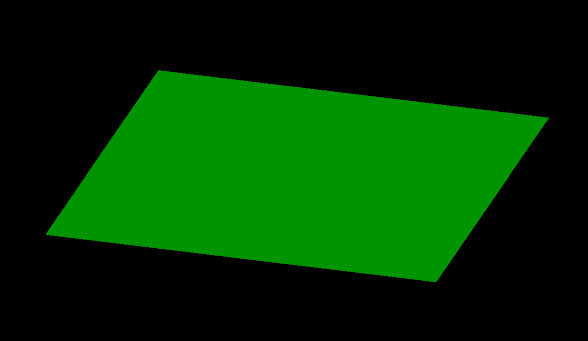
In the example below, we construct a simple, flat grid surface.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface

project = Project()

with project.new("surfaces/grid", GridSurface(
    major_dimension_count=360,
    minor_dimension_count=360,
    x_step=1, y_step=1, start=[0, 0, 0])) as grid:
    grid

If you run the above code, you should generate an object that looks like this:

Creating a grid surface with z-coordinates

After you create a grid surface, you can adjust its elevation by setting the z-coordinate of each point. Keeping the function of setting the z-coordinate separate from setting the point’s x and y coordinates is useful because it saves the script writer the effort of regenerating the x and y coordinates. It is also useful for creating three dimensional representations of equations where the z coordinate is calculated based on the x and y coordinates.

In the example below, we:

Copy the GridSurface created in the previous section.
Modify the z-coordinate of the copied GridSurface where z = 40 * sin(x + y). The x and y coordinates are interpreted as the angles in degrees.

from mapteksdk.project import Project
import numpy

project = Project()

input_path = "/surfaces/grid"
output_path = "/surfaces/sine_grid"

copy = project.copy_object(input_path, output_path)

with project.edit(output_path) as sine_grid:
    theta = numpy.deg2rad(sine_grid.points[:, 1])
    phi = numpy.deg2rad(sine_grid.points[:, 2])
    sine_grid.point_z = numpy.sin(theta + phi)
    # Multiply the z by forty to make it easier to see.
    sine_grid.point_z *= 40

If you run the above code, you should generate an object that looks like this:

Creating irregular grids

The GridSurface class is not limited to storing regular grids. You can use a GridSurface to represent irregular grids. An irregular grid is a grid where cells are unevenly spaced.

Note: When constructing this type of grid, the x_step, y_step and start parameters should be omitted from the constructor.

The following example demonstrates how to create an irregular grid surface with 5 rows and 4 columns.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface
import numpy

project = Project()

points = numpy.array([
  (0, 4.9, 4.9), (1, 5.1, 4.4), (1.9, 5.1, 3.4), (3, 5, 3),
  (0.1, 4.1, 3.9), (0.9, 4.1, 4.1), (2.1, 4, 2.9), (3.1, 4.1, 2.5),
  (0.1, 3.1, 3.4), (1, 3.1, 3.4), (2, 3, 2.4), (3.1, 3, 2.1),
  (0.1, 1.9, 2.5), (0.9, 2, 2.6), (2, 2.1, 1.9), (3.1, 1.9, 1.4),
  (-0.1, 1, 1.9), (0.9, 0.9, 1.5), (2, 1.1, 1), (3.1, 1.1, 0.9)
])

with project.new("surfaces/irregular_grid", GridSurface(
    major_dimension_count=5,
    minor_dimension_count=4)) as irregular_grid_surface:
  irregular_grid_surface.points = points

If you run the above code, you should generate an object that looks like this:

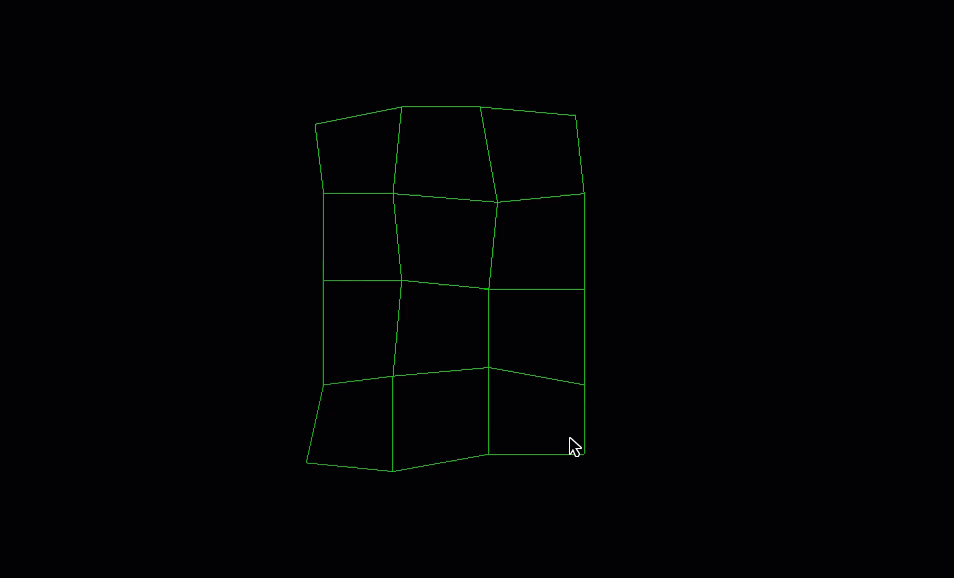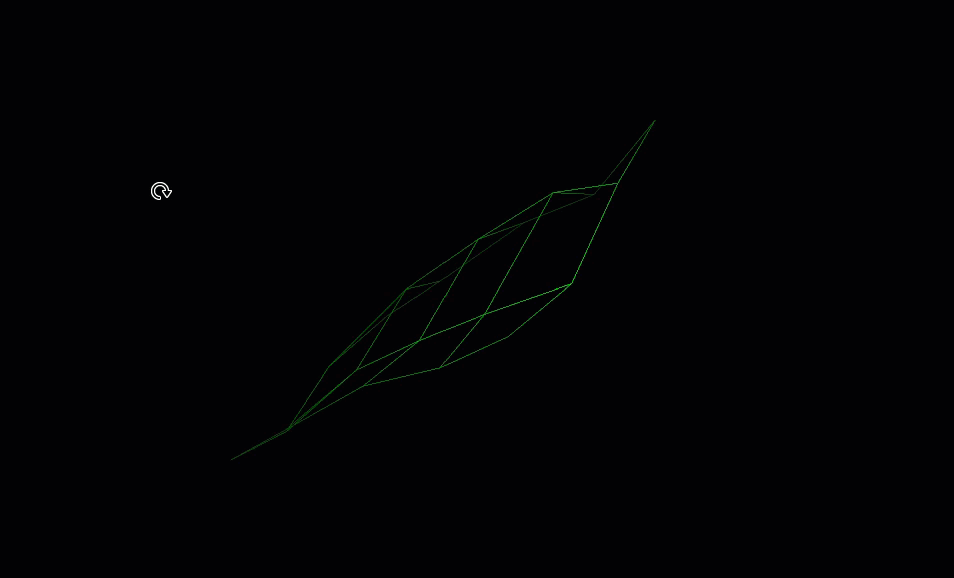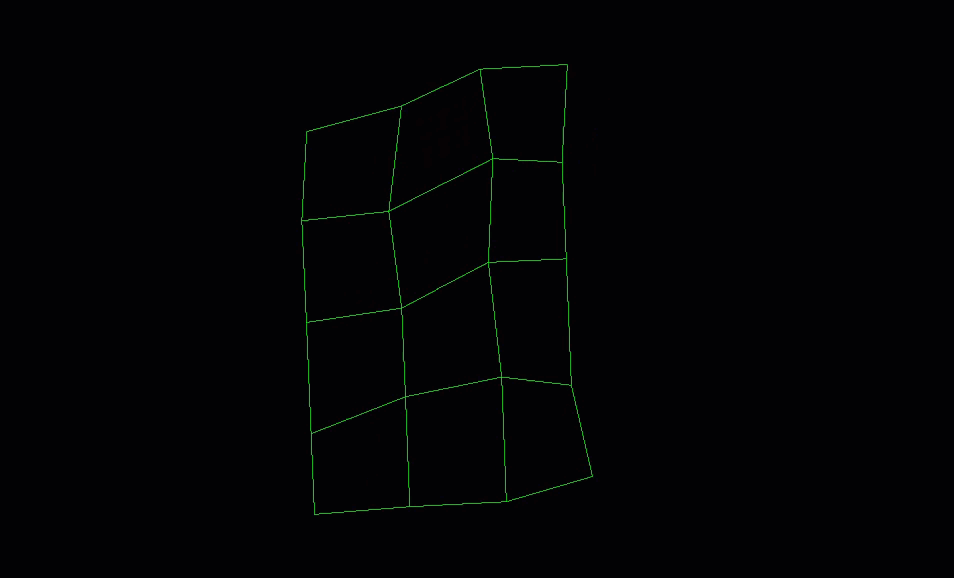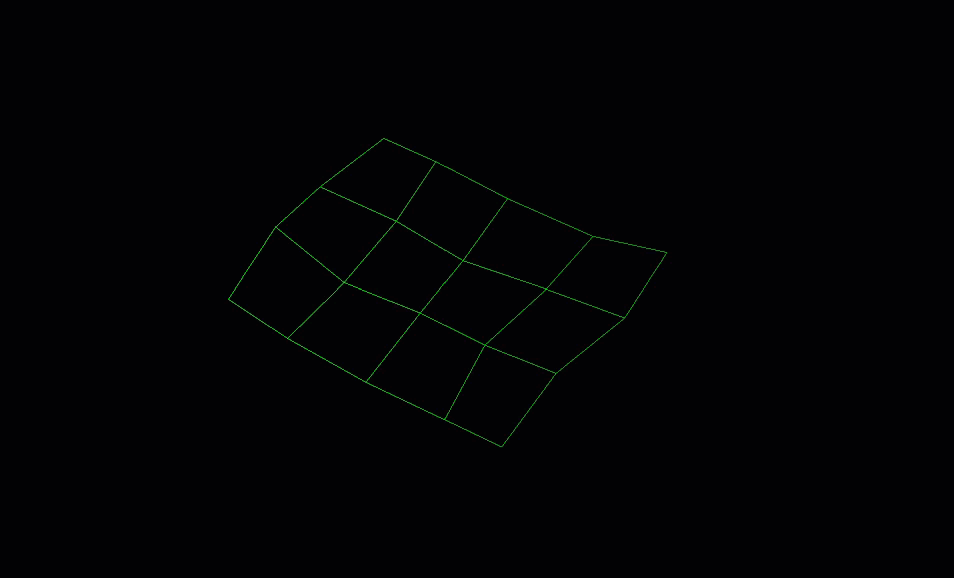
Colouring the points of a grid surface

You can colour the points of a GridSurface object using the point_colours property. The following example demonstrates how to colour the points of a grid surface by setting all points to a single colour.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface

project = Project()


with project.new("surfaces/grid_single_colour", GridSurface(
    major_dimension_count=5, minor_dimension_count=5,
    x_step=0.5, y_step=0.5
    )) as grid:
    grid.point_colours = [[0,0,255]]

If you run the above code, you will generate an object that looks like this:

Colouring a grid surface with a colour map

The easiest way to colour a GridSurface is to use a colour map. The following example shows how to create and apply a colour map to a GridSurface.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface, NumericColourMap

project = Project()

with project.new("legends/numeric_grid_map", NumericColourMap) as colour_map:
  colour_map.interpolated = False
  colour_map.ranges = [-0.5, 0.5, 1.5, 2.5, 3.5]
  colour_map.colours = [[255, 0, 0, 255], [0, 255, 0, 255],
                        [0, 0, 255, 255], [255, 0, 255, 255]]
  colour_map.lower_cutoff = [0, 0, 0, 120]
  colour_map.upper_cutoff = [0, 0, 0, 120]

with project.new("surfaces/grid_numeric_colour_map", GridSurface(
    major_dimension_count=5, minor_dimension_count=5,
    x_step=0.5, y_step=0.5
    )) as grid:
  grid.point_attributes["value"] = [3, 2, 2, 1, 0,
                                    2, 2, 3, 0, 1,
                                    1, 3, 0, 2, 2,
                                    2, 0, 1, 3, 2,
                                    0, 1, 2, 2, 3]
  grid.point_attributes.set_colour_map("value", colour_map)

If you run the above code, you should generate an object that looks like this:

Setting cell visibility

You can set make cells in a GridSurface visible or invisible. The following example demonstrates how to manipulate the visibility of cells in a GridSurface.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface

project = Project()

visibility = [True, True, False, True,
              False, False, True, True,
              True, True, True, False,
              True, False, True, False]

# The negative y step flips the cell network such that the
# 0th row is at the top and the last row is at the bottom.
with project.new("surfaces/grid_cell_visibility", GridSurface(
    major_dimension_count=5, minor_dimension_count=5,
    x_step=1, y_step=-1
    )) as grid:
  grid.cell_visibility = visibility

If your run the above code, you should generate an object that looks like this:

Setting point visibility

You can use the point_visibility property to make the points in a GridSurface visible or invisible. A cell that contains points that are invisible will not appear in the view. We demonstrate this in the example below:

from mapteksdk.project import Project
from mapteksdk.data import GridSurface

project = Project()

visibility = [True, True, False, True, True,
              False, True, True, True, True,
              True, True, True, False, False,
              True, False, True, True, False,
              False, True, True, True, True]

with project.new("surfaces/grid_point_visibility", GridSurface(
    major_dimension_count=5, minor_dimension_count=5,
    x_step=1, y_step=1
    )) as grid:
  grid.point_visibility = visibility

If you run the above code, you will generate an object that looks like this:

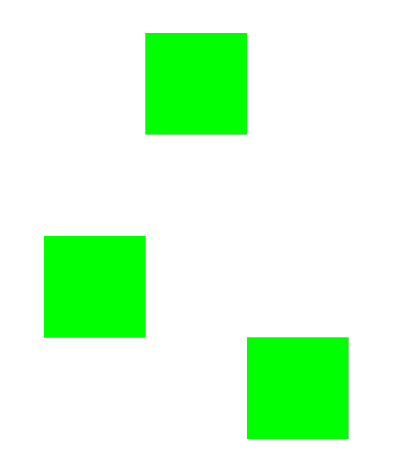
If you view the object in points mode (and overlay the above image), it will look like this:

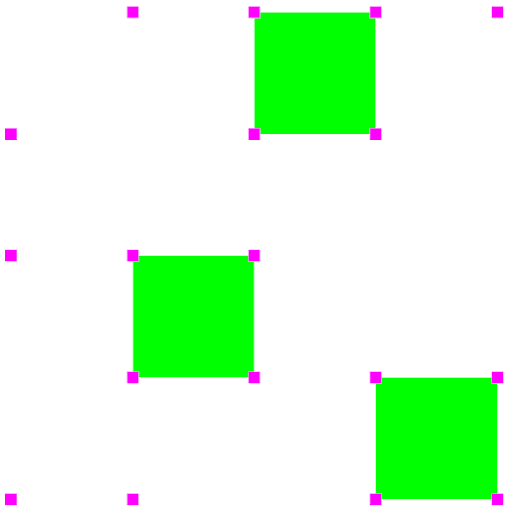
As you can see, every cell that is visible contains four visible corners.

Colouring points using point selection

GridSurface objects support point selection just as other point-based objects. This allows for scripts to operate on a selection of points of a GridSurface rather than the entire surface. This is demonstrated in the example below where selected points are coloured a single colour.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface
from mapteksdk.pointstudio.operations import object_pick

project = Project()

oid = object_pick(label="Pick a grid surface to colour selected points")

if not oid.is_a(GridSurface):
  raise ValueError("You must pick a GridSurface.")

with project.edit(oid) as grid:
  grid: GridSurface
  grid.point_colours[grid.point_selection] = [221, 160, 221, 255]

Here is an example of the type of object you can generate using the above code:

Compare this with the original object selected that was created in the section Colouring the Points of a GridSurface:

Colouring points using cell selection

You can apply operations to a selected number of cells in a GridSurface . In the example below, the selected cells are made invisible.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface
from mapteksdk.pointstudio.operations import object_pick

project = Project()

oid = object_pick(label="Pick a grid surface to hide selected cells")

if not oid.is_a(GridSurface):
  raise ValueError("You must pick a GridSurface.")

with project.edit(oid) as grid:
  grid: GridSurface
  grid.cell_visibility[grid.cell_selection] = False

Here is an example of the type of object you can generate using the above code:

Compare this with the original object selected that was created in the section Colouring the Points of a GridSurface:

Adding cell attributes to a GridSurface

You can create attributes at a cellular level. These are called cell attributes. Every cell shares the same cell attributes. The example below demonstrates:

Three different ways to generate cell attributes
How to colour the points of the GridSurface based on the cell attributes

import numpy
from mapteksdk.project import Project
from mapteksdk.data import GridSurface

points = numpy.array([
  [[-0.1, 4.9, -0.1], [1, 5, 0.2], [1.9, 5.2, 0], [2.9, 4.8, 0.2]],
  [[0, 4, -0.1], [0.8, 3.9, 0], [2.2, 4, 0.1], [3.2, 3.9, -0.2]],
  [[-0.1, 2.9, 0], [1.2, 2.8, 0], [2, 2.9, 0], [2.9, 2.9, 0.1]],
  [[0.1, 2, 0.1], [1.2, 1.9, 0.2], [2, 1.9, -0.1], [3.2, 1.8, 0]],
  [[0.2, 1.1, -0.2], [0.8, 0.9, 0.1], [2.1, 0.9, -0.2], [3.2, 1.2, 0]]
])

depth = [13.74216711, 6.26654481, 11.17255728, 10.50674182,
         7.96397555, 8.89378882, 12.19867618, 8.01683923,
         5.25515135, 6.55541477, 12.89572386, 12.29907013]

project = Project()

with project.new("surfaces/grid_with_cell_attribute", GridSurface(
    major_dimension_count=points.shape[0],
    minor_dimension_count=points.shape[1])) as grid_surface:
  grid_surface: GridSurface
  grid_surface.cell_points[:] = points

  # Calculate the area of all cells.
  cell_areas = numpy.empty((grid_surface.cell_count), numpy.float64)
  for i, cell in enumerate(grid_surface.cells):
    p0, p1, p2, p3 = grid_surface.points[cell]
    # Assuming the cell is not degenerate the points are like this:
    # p3 o---------o p2
    #    |         |
    #    |         |
    #    |         |
    # p0 o---------o p1

    area = 0

    # The squared length of the diagonals.
    diagonal_1 = numpy.sum(numpy.square(p0 - p2))
    diagonal_2 = numpy.sum(numpy.square(p1 - p3))

    # Calculate the area using the shorter diagonal.
    # This ensures correct results for concave cells.
    # This still gives incorrect values for degenerate cells.
    if diagonal_1 < diagonal_2:
      area += numpy.linalg.norm(numpy.cross(p1 - p0, p2 - p0))
      area += numpy.linalg.norm(numpy.cross(p2 - p0, p3 - p0))
    else:
      area += numpy.linalg.norm(numpy.cross(p0 - p1, p3 - p1))
      area += numpy.linalg.norm(numpy.cross(p2 - p1, p3 - p1))
    area /= 2
    cell_areas[i] = area

  # The depth attribute values are hard-coded into the script.
  grid_surface.cell_attributes["depth"] = depth
  # The area attribute values are calculated based on the geometry.
  grid_surface.cell_attributes["area"] = cell_areas
  # The volume attribute values are calculated based on other attributes.
  grid_surface.cell_attributes["volume"] = (
    grid_surface.cell_attributes["area"]
    * grid_surface.cell_attributes["depth"])

# Colour grid surface points based on cell  attributes
  for i, cell in enumerate(grid_surface.cells):
    a, b, c, d = cell
    cell_volume =  grid_surface.cell_attributes["volume"][i]
    if cell_volume > 7 and cell_volume < 10:
      grid_surface.point_colours[a] = [255,0,0,255]
      grid_surface.point_colours[b] = [255,0,0,255]
      grid_surface.point_colours[c] = [255,0,0,255]
      grid_surface.point_colours[d] = [255,0,0,255]
    else:
      grid_surface.point_colours[a] = [0,0,255,255]
      grid_surface.point_colours[b] = [0,0,255,255]
      grid_surface.point_colours[c] = [0,0,255,255]
      grid_surface.point_colours[d] = [0,0,255,255]

If you run the above code, you will generate an object that looks like this:

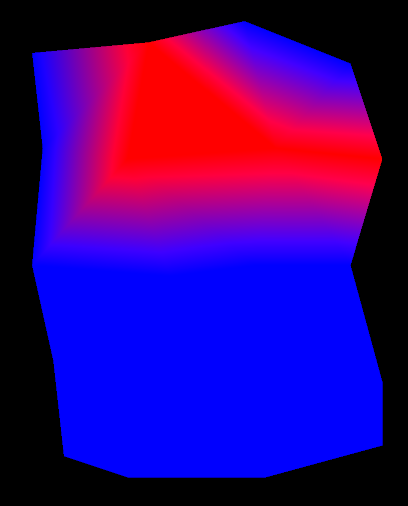
The resulting GridSurface from the above code has three cell attributes:

Depth, where the values are provided by the script.
Area, where the values are calculated based on the topology of the grid surface.
Volume, which is calculated based on the other cell attributes — it is the depth multiplied by the area.

Note: The volume is calculated at run-time and not dynamically. This means that if you make a change to the depth or the area cell attributes, the volume will not be updated.

Comparing points and cell points of a GridSurface

You can manipulate a GridSurface by either setting its points or cell points.

Below are two scripts — one that creates a GridSurface using points and one that creates a GridSurface using cell points. Using cell points is the preferred method as it preserves the structure of the GridSurface.

from mapteksdk.project import Project
from mapteksdk.data import GridSurface

project = Project()

with project.new("surfaces/stepped_points", GridSurface(
    major_dimension_count=14, minor_dimension_count=10,
    x_step=1
    )) as grid:
  row_width = grid.minor_dimension_count
  height = 0
  y = 0
  for i, start in enumerate(range(0, grid.point_count, row_width)):
    grid.points[start:start + row_width, 2] = height
    grid.points[start:start + row_width, 1] = y
    if i % 2 == 1:
      height += 1
    else:
      y += 1

from mapteksdk.project import Project
from mapteksdk.data import GridSurface

project = Project()

with project.new("surfaces/stepped_cell_points", GridSurface(
    major_dimension_count=14, minor_dimension_count=10,
    x_step=1
    )) as grid:
  height = 0
  y = 0
  for i, row in enumerate(grid.cell_points):
    row[:, 2] = height
    row[:, 1] = y
    if i % 2 == 1:
      height += 1
    else:
      y += 1

Running one of the above scripts in this section will generate an object that looks like this: