Subblocked Block Models
A subblocked block model is a type of block model that allows for the division of parent blocks into smaller, more detailed subblocks. In areas where a block is split into subblocks, more detail is stored. In areas where the parent block is not split, less detail is stored. A subblocked block model is represented in the SDK with the SubblockedBlockModel class.
Parent blocks and subblocks
Parent blocks are defined when the model is created and cannot be changed once they are defined. They are based on the parameters passed to the constructor and are arranged into rows, columns and slices. All parent blocks in a block model are of the same size.
In a subblocked block model, each parent block can be split into multiple subblocks that fill its volume. A parent block can also contain no subblocks. A parent block with no subblocks indicates either there is nothing of interest within its volume, or what is within its volume is unknown.
Subblocks are smaller blocks (sometimes called child blocks) within a parent block. Note the following properties of subblocks:
-
Subblocks can be added and deleted from the model after it is created.
-
Subblocks can have different sizes.
-
Subblocks must be equal in size or smaller than the primary blocks of the model.
-
There can be multiple subblocks within one primary block.
-
If a primary block contains subblocks, they should completely fill the volume of the primary block.
-
Block attributes have one value for each subblock.
-
Subblocks that are not inside the model extent do not appear when the model is viewed.
Subblocks are created using the add_subblocks() method. This method has two parameters: centroid and size. You can use the SubblockedBlockModel.add_subblocks() method to add subblocks to a SubblockedBlockModel, even after the model has been created. To be viewed, these blocks need to be added within the extent of the block model.
Subblocked block model examples
The following examples demonstrate how to work with subblocked block models using the SDK.
Adding subblocks to a subblocked block model
The following example demonstrates how to add subblocks to a subblocked block model. In this example, subblocks are defined by specifying their centroids and sizes, and then adding them to a newly created SubblockedBlockModel.
from mapteksdk.project import Project
from mapteksdk.data import SubblockedBlockModel
centroids = [[-1.5, -1, -1], [-0.5, -1, -1], [-1, 1, -1],
[-1.5, -1, 1], [-0.5, -1, 1], [-1, 1, 1],
[-1.5, -1, 3], [-0.5, -1, 3], [-1, 1, 3]]
sizes = [[1, 2, 2], [1, 2, 2], [2, 2, 2],
[1, 2, 2], [1, 2, 2], [2, 2, 2],
[1, 2, 2], [1, 2, 2], [2, 2, 2]]
project = Project()
with project.new("blockmodels/subblockmodel", SubblockedBlockModel(
x_count=1, y_count=2, z_count=3, x_res=4, y_res=4, z_res=4
)) as new_blocks:
new_blocks.origin = [94, -16, 12]
new_blocks.add_subblocks(centroids, sizes)
Running this script will generate a SubblockedBlockModel that looks like this:

Rotating and translating a subblocked block model
By default, a SubblockedBlockModel is axis aligned and has its origin located at [0, 0, 0]. However, the data represented by a SubblockedBlockModel is often not axis-aligned and not located at the origin. To accurately position and orient the model, you may need to rotate and translate it.
The following example demonstrates how to create a SubblockedBlockModel, rotate it 30 degrees around the X axis and 45 degrees around the Y axis, and then translate it 5 metres in the X direction and 3 metres in the Y direction.
import math
from mapteksdk.project import Project
from mapteksdk.data import SubblockedBlockModel, Axis
centroids = [[0, 0, 0], [0, 2, 0], [2, 2, 0],
[1.5, -0.5, 0], [1.5, 0.5, 0],
[2.5, -0.5, 0], [2.5, 0.5, 0],
[-0.5, -0.5, 1], [-0.5, 0.5, 1],
[0.5, -0.5, 1], [0.5, 0.5, 1],
[0, 2, 1], [2, 2, 1]]
sizes = [[2, 2, 1], [2, 2, 1], [2, 2, 1],
[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1],
[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1],
[2, 2, 1], [2, 2, 1]]
project = Project()
with project.new("blockmodels/rotated_subblocked", SubblockedBlockModel(
x_count=2, y_count=2, z_count=2, x_res=2, y_res=2, z_res=1
)) as new_rotated_model:
new_rotated_model: SubblockedBlockModel
new_rotated_model.rotate(math.radians(30), Axis.X)
new_rotated_model.rotate(math.radians(45), Axis.Y)
new_rotated_model.origin = [5, 3, 0]
# Note: It is more efficient to perform all rotations and translations
# on a block model before adding the subblocks.
new_rotated_model.add_subblocks(centroids, sizes)
print(new_rotated_model.block_centroids)
Running this script will result in a model that looks like this:

The unrotated version of the model looks like this:

The following printed output will also result:
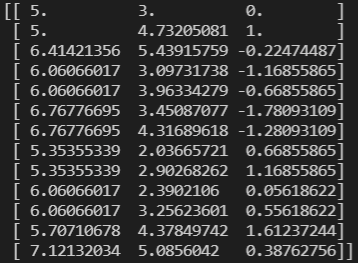
The two SubblockedBlockModel instances are identical apart from their rotation and origin. However, you may notice that the centroids of the rotated model differ from those passed to the SubblockedBlockModel.add_subblocks() method. This discrepancy occurs because the method assumes that the coordinates are provided in block coordinates (or model coordinates). This means that the coordinates are relative to the model’s origin and rotation rather than the project’s origin. The concept of block coordinates is explained in more detail in the following section.
By default, the rotation and translation of the model are managed automatically by the Maptek Python SDK, allowing you to use the same centroids for both rotated and unrotated block models.
Positioning a subblocked block model using world coordinates or block coordinates
Every block model has its own coordinate system called the block coordinate system (or the model coordinate system). By default, the SubblockedBlockModel.add_subblocks() method assumes the block centroids are specified in the block coordinate system. The block coordinate system has the following properties:
-
[0, 0, 0] in the block coordinate system is the origin of the block model. This is located in the centre of the block in the 0th row, column and slice.
-
The x direction is aligned to the columns of the model.
-
The y direction is aligned to the rows of the model.
-
The z direction is aligned to the slices of the model.
If a model is located at the origin and not rotated, the world and block coordinate systems are the same.
Adding subblocks in world coordinates
If the centroids of the subblocks are already in world coordinates (for example, if they were read from a CSV containing world coordinates) then it is not necessary to convert them to block coordinates when adding the subblocks to a model. Instead, set the use_block_coordinates flag of the SubblockedBlockModel.add_subblocks() method to False to indicate that the centroids are in world coordinates.
In the example below, we copy the model created in the previous example and then subblocks to the model in world coordinates by setting the use_block_coordinates flag of the SubblockedBlockModel.add_subblocks() method to False.
Note: The next example only copies the topology of the block model and does not copy the block attributes. Use Project.copy_object() to perform a full copy.
from mapteksdk.project import Project
from mapteksdk.data import SubblockedBlockModel
project = Project()
with project.read("blockmodels/rotated_subblocked") as original:
with project.new("blockmodels/rotated_subblocked_copy",
SubblockedBlockModel(
x_count=2, y_count=2, z_count=2, x_res=2, y_res=2, z_res=1
)) as copy:
# Use the orientation property to copy the rotation of the original
# model.
copy.set_orientation(*original.orientation)
# Now copy the origin and blocks.
copy.origin = original.origin
# use_block_coordinates=False indicates that block centroids
# are in world coordinates and not block coordinates.
copy.add_subblocks(
original.block_centroids,
original.block_sizes,
use_block_coordinates=False)
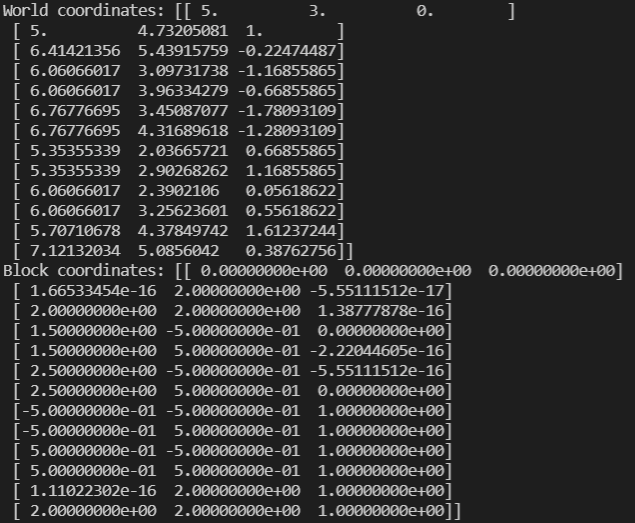
print("World coordinates:", original.block_centroids)
print("Block coordinates:", original.convert_to_block_coordinates(original.block_centroids))
Running this code will copy the block model from the previous example and print its world and block coordinates, which should look like this:
Colouring a subblocked block model using a colour map
The following example demonstrates how to colour a SubblockedBlockModel using a colour map.
from mapteksdk.project import Project
from mapteksdk.data import StringColourMap, SubblockedBlockModel
project = Project()
centroids = [[0, 0, 0], [0, 2, 0], [2, 2, 0],
[1.5, -0.5, 0], [1.5, 0.5, 0],
[2.5, -0.5, 0], [2.5, 0.5, 0],
[-0.5, -0.5, 1], [-0.5, 0.5, 1],
[0.5, -0.5, 1], [0.5, 0.5, 1],
[0, 2, 1], [2, 2, 1]]
sizes = [[2, 2, 1], [2, 2, 1], [2, 2, 1],
[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1],
[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1],
[2, 2, 1], [2, 2, 1]]
with project.new("blockmodels/coloured_subblocked", SubblockedBlockModel(
x_count=2, y_count=2, z_count=2, x_res=2, y_res=2, z_res=1
)) as model:
model.add_subblocks(centroids, sizes)
# Create a colour map.
with project.new(None, StringColourMap) as string_map:
string_map.legend = ["red", "green", "blue", "yellow", "cyan", "magenta"]
string_map.colours = [[255, 0, 0, 255], [0, 255, 0, 255],
[0, 0, 255, 255], [255, 255, 0, 255],
[0, 255, 255, 255], [255, 0, 255, 255]]
string_map.cutoff = [0, 0, 0, 200]
# Set the colour of each block.
model.block_attributes["colour"] = ["red", "green", "blue", "yellow",
"cyan", "magenta", "red", "green",
"blue", "yellow", "cyan", "magenta",
"red"]
# Use the colour map to colour the model.
model.block_attributes.set_colour_map("colour", string_map)
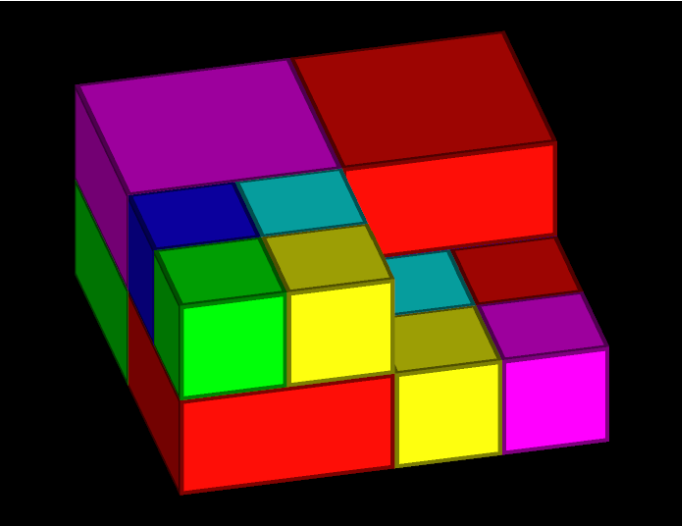
Running this code will generate a SubblockedBlockModel that is coloured according to the specified colour map. The colours are applied based on the attributes assigned to each block, with the colour map translating these attributes into visible colours.
Querying which parent blocks contain subblocks
The following example demonstrates a way of identifying which parent blocks in a SubblockedBlockModel contain subblocks using the block_to_grid_index property. In the example, we map a subblock from its index to the column, row and slice of the parent block that contains the subblock.
from mapteksdk.project import Project
from mapteksdk.pointstudio.operations import object_pick
project = Project()
oid = object_pick(label="Select a subblocked block model")
with project.read(oid) as model:
block_to_grid_index = model.block_to_grid_index
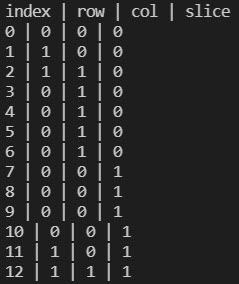
print("index | row | col | slice")
for i, index in enumerate(block_to_grid_index):
col = index[0]
row = index[1]
slice_ = index[2]
print(f"{i} | {int(row)} | {int(col)} | {int(slice_)}")
Running this script and selecting the subblocked block model from the previous example will indicate which parent blocks contain subblocks by mapping each subblock to its parent block’s coordinates in the grid. The output will show the index of each subblock along with its corresponding row, column, and slice in the parent block model.
Locating subblocks and setting their visibility
You can use the SubblockedBlockModel.grid_index() property to obtain all the subblocks contained within a specific parent block as determined by its row, column and slice. This method allows you to perform operations on all subblocks within a given parent block, treating the subblocked model as a dense block model.
The following example demonstrates how to locate all subblocks within the parent block located at row 0, column 0, and slice 1, and then set their visibility to false:
from mapteksdk.project import Project
from mapteksdk.data import SubblockedBlockModel
project = Project()
centroids = [[0, 0, 0], [0, 2, 0], [2, 2, 0],
[1.5, -0.5, 0], [1.5, 0.5, 0],
[2.5, -0.5, 0], [2.5, 0.5, 0],
[-0.5, -0.5, 1], [-0.5, 0.5, 1],
[0.5, -0.5, 1], [0.5, 0.5, 1],
[0, 2, 1], [2, 2, 1]]
sizes = [[2, 2, 1], [2, 2, 1], [2, 2, 1],
[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1],
[1, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 1],
[2, 2, 1], [2, 2, 1]]
with project.new("blockmodels/visible_model", SubblockedBlockModel(
x_count=2, y_count=2, z_count=2, x_res=2, y_res=2, z_res=1
)) as model:
model.add_subblocks(centroids, sizes)
target_parent_block = [0, 0, 1]
grid_index = model.grid_index(target_parent_block)
model.block_visibility[grid_index] = False
Running the script will create a model where all subblocks within the parent block at [0, 0, 1] are set to be invisible, as shown in the animation below:

The resulting model is the same as the one generated in the section Colouring SubblockedBlockModels using a colour map.
Subblocked block models with topological errors
When creating a new SubblockedBlockModel, it is possible for the model to contain topological errors. These errors can cause issues with algorithms run on the model leading to erroneous results. This section covers several of the common topological errors that can occur and how to avoid them.
Subblocks outside of the block extent
If a subblock is not completely contained within a parent block, it will not appear when the model is viewed. When creating a SubblockedBlockModel, make sure that the subblocks are within a parent block.
The following code demonstrates how to calculate the extents of a SubblockedBlockModel.
from mapteksdk.data.blocks import SubblockedBlockModel
import numpy
from mapteksdk.project import Project
project = Project()
with project.read("blockmodels/rotated_subblocked") as model:
model: SubblockedBlockModel
# [0, 0, 0] in block coordinates is the centre of the block in row 0,
# column 0 and slice 0. This means that the block model extends for
# half a block below [0, 0, 0].
minimum = -0.5 * model.block_resolution
# This is effectively number of blocks in each dimension * size of
# each block in each dimension. This is then offset by half a block to
# compensate for the minimum not being located at [0, 0, 0].
maximum = (numpy.array([model.column_count, model.row_count,
model.slice_count]) - 0.5) * model.block_resolution
world_minimum = model.convert_to_world_coordinates([minimum])
world_maximum = model.convert_to_world_coordinates([maximum])
print("Extents in block coordinates")
print("Minimum: ", minimum)
print("Maximum: ", maximum)
print("Extents in world coordinates")
print("Minimum: ", world_minimum)
print("Maximum: ", world_maximum)
If you run the above code and have previously run this example, you should generate the following output:
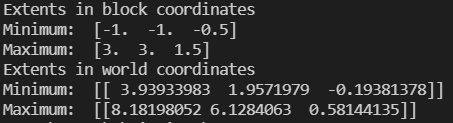
The most common mistake that leads to blocks outside of the model extent is failing to compensate for the half block offset. The origin of a block model is located in the centre of the block in the zeroth row, column and slice and not in the bottom corner of the model. This means that the block model extends half a block below the origin. Failing to compensate for this half block offset usually causes the blocks in the last row, slice and column to fail to appear when the model is viewed. This issue can be fixed by adjusting all of the block centroids by half a block to compensate for this offset. Other cases are more difficult to fix and require carefully checking the extents of the blocks against the extents of the model.
Overlapping Blocks
Another common error that can occur when creating a subblocked block model is overlapping blocks. In the view, these blocks will appear on top of each other with each block fighting to be on top of the other (referred to as z-fighting). To resolve this, the offending subblocks should be removed and replaced with blocks that do not overlap.
Given an arbitrary block model, calculating if any blocks overlap can be a computationally expensive operation especially for large models. It requires comparing the extents of every block to every other block to determine if any overlap. Because of this, the SDK does not attempt to automatically check if a model contains overlapping blocks.
Subblocks that do not fully fill the parent block
If a parent block contains subblocks, then the subblocks should completely fill the parent blocks. However the SDK contains no safeguards against having a parent block not completely filled with subblocks. Creators of SubblockedBlockModel should be careful to ensure they do not accidentally create models with holes in parent blocks.
