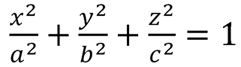Using Coordinate Systems
Background
The Earth's surface is actually an irregular shape - not an ideal ball or sphere. Actually the Earth - land and sea - is continuously changing shape, influenced by factors such as its rotation, gravity and tectonic movement. A number of methods are used to create 3D representations of the entire Earth as well as local regions. The most basic representation involves a flattened sphere or ellipsoid. Once a representation is chosen, a coordinate system can be defined to assist in specifying surface location and height levels. Different approaches have been developed for different applications and technologies. Generally, swapping between coordinate systems will entail calculating a new set of equivalent coordinates for points under investigation.
Related commands:
Ellipsoids
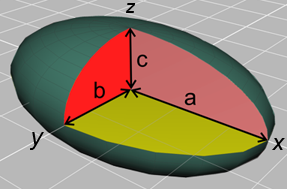
Ellipsoid include flattened spheres which can be represented mathematically using different length radii
|
|
|
|
Representation of an ellipsoid centred at the origin of a Cartesian coordinate system and aligned with the x, y, z axes. The semi-principal axes are of length a, b, c. They correspond to the semi-major axis (longer) and semi-minor axis (shorter) of the appropriate ellipses they create along each x, y, z axis. |
The standard equation of an ellipsoid centred at the origin of a Cartesian coordinate system and aligned with the x, y, z axes.
|
The Earth can be simply approximated by an ellipsoid with a greater radius around the tropics - allowing for the accumulation of water due to centrifugal forces caused by the Earth spinning on it's polar axis (this particular ellipsoid can also be termed a spheroid). However, due to the irregularity of the actual Earth's surface and sea levels, localised ellipsoids have also been used to give better fitting approximations for various regions around the Earth.
WGS 84 is a World Geodetic System that includes a reference ellipsoid representing the whole Earth. Other examples include the International Ellipsoid of 1924, GRS80 Ellipsoid, Clarke Ellipsoid of 1866, Australian National Spheroid.
| Ellipsoids | ||

|


|

|
| Sphere: a = b = c |
Spheroid: a = b > c (approximates Earth shape better than a sphere) |
Tri-axial: a > b > c |
Geoid
The geoid is the shape that the surface of the oceans would take under the influence of Earth's gravitation and rotation alone, in the absence of other influences such as winds and tides. This surface is extended through the continents. All points on the geoid have the same gravity potential energy (the sum of gravitational potential energy and centrifugal potential energy). The force of gravity acts everywhere perpendicular to the geoid, meaning that plumb lines point perpendicular and water levels parallel to the geoid. The geoid is actually quite irregular because anomalies exist in the Earth's gravitational field at many locations for various reasons. The result resembles a 'lumpy' spheroid.
Spherical harmonics are often used to approximate the 3D shape of the geoid. The current best such set of spherical harmonic coefficients is EGM96 (Earth Gravity Model 1996).
| Earth Models | ||
|
|
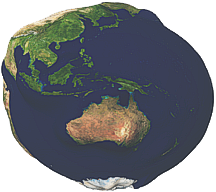
|
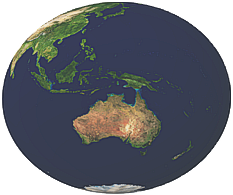
| Sphere - for simple cases. | Ellipsoid (Spheroid) - better fitting (mathematical) approximation. | Geoid - attempts to accurately represent Mean Sea Level, including gravitational anomalies that have been discovered and continues these equivalent levels through land masses as well. Very hard to model mathematically. |
Datums & Projections
A datum is a system which allows the location of latitudes and longitudes (and heights) to be defined on the surface of the Earth, generally represented by an ellipsoid.
A projection is a process that uses the latitude and longitude ‘drawn’ on the surface of the Earth using a datum, to be ‘drawn’ onto a ‘flat piece of paper’ that is called a map.
All projections result in some distortion of the relationships between features on the sphere when they are projected onto a flat surface.
Projection distortions include:
- direction between features
- distance between features
- shape of any feature
- size of any feature
Using the concept of an imaginary ‘piece of paper’ touching the Earth there are three basic techniques used to create a projection and therefore a map. These are:
- azimuthal: If the imaginary 'piece of paper' is flat, it is usually over the Polar areas.
- conical: If the imaginary 'piece of paper' is rolled into a cone, it is usually placed over the mid-lattitude areas.
- cylindrical: If the imaginary 'piece of paper' is rolled into a cylinder, it is usually used over Equatorial areas or for World Maps.
The Mercator projection is a cylindrical map projection presented by the Flemish geographer and cartographer Gerardus Mercator in 1569. It became the standard map projection for nautical purposes because of its ability to represent lines of constant course. Although the linear scale is equal in all directions around any point, thus preserving the angles and the shapes of small objects (which makes the projection conformal), the Mercator projection distorts the size of objects as the latitude increases from the Equator to the poles. So, for example, landmasses such as Greenland and Antarctica appear much larger than they actually are relative to land masses near the equator, such as Central Africa.
UTM
The Universal Transverse Mercator (UTM) conformal projection uses a 2-dimensional Cartesian coordinate system to give locations on the surface of the Earth. Like the traditional method of latitude and longitude, it is a horizontal position representation, i.e. it is used to identify locations on the Earth independently of vertical position. However, it differs from that method in several respects. The UTM system is not a single map projection. The system instead divides the Earth into sixty zones, each being a six-degree band of longitude, and uses a secant transverse Mercator projection in each zone.
In the UTM system, east-west distances are called eastings and are measured in metres from the central meridian in each UTM zone. Eastings measured east from that line are positive, and eastings west from that line are negative.
To get around the problem of negative eastings, a false origin is used which is 500 000 m west of the central meridian. This adjustment, called False Easting, adds 500 000 m to all eastings. For example, suppose a place is 400 km, or 400 000 m, west of the central meridian. The nominal easting of the place is -400 000 m. We add 500 000 to this figure to get a positive "corrected" easting of 100 000 m.
The situation for north-south distances, or northings is similar. In the UTM system these are measured in metres from the Equator and are positive north and negative south. To avoid negative northings, 10 000 000 m are added to northings in the Southern Hemisphere. In other words, in the Southern Hemisphere we have a false origin for northings which is 10 000 000 m south of the Equator. This adjustment is called False Northing.
| Universal Transverse Mercator
(UTM) 3D view and 2D projection over Australia |

|
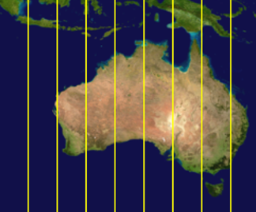
|
| Each vertical sector represents an independent zone that uses an individual transverse Mercator projection. The amount of distortion is held below 1 part in 1000. |
Vertical Datums
For generations, the only way to express topographic or bathymetric elevation was to relate it to sea level. Geodesists once believed that the sea was in balance with the earth's gravity and formed a perfectly regular figure. Mean Sea Level (MSL) is usually described as a tidal datum that is the arithmetic mean of hourly water elevations observed over a long period. MSL is defined as the zero elevation for a local area. This zero surface is called a vertical datum.
Unfortunately for mapmakers, sea level is not a simple surface and is more closely related to the geoid than an ellipsoid. Although for practical purposes, at the coastline the geoid and MSL surfaces are often assumed to be the same, at some spots the geoid can actually differ from MSL by several metres.
GPS has transformed how altitude at any location is measured. However, GPS uses an ellipsoid coordinate system for both its horizontal and vertical datums. Thus, GPS will return an Ellipsoid Height based on a reference ellipsoid (not MSL), and then require an offset value (called Geoid Height) to calculate actual topographic height (above MSL) at a location.
| Height relationships between Earth models and main features |
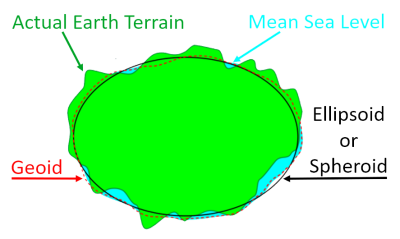
|

|
|
H = height with respect to the Geoid h = height with respect to the Ellipsoid or Spheroid N = separation or difference between the Geoid and Ellipsoid or Spheroid height. This is a correction factor that can be applied to GPS readings (which use Ellipsoid height) to calculate height above Mean Sea Level or the Geoid. AUSGeoid09 is an example of a list of these correction factors that covers Australia. |
| Note that the Geoid datum can be either below or above the Ellipsoid or Spheroid datum. |
| Note that Mean Sea Level might not match perfectly with the Geoid. |
| Note that Mean Sea Level might not be at the same level around a coastline. For example, Australia and New Zealand have recorded slight variations around their coastlines, and have used these to produce new height datums. |
EPSG Dataset
The International Association of Oil and Gas Producers (IOGP) has produced the EPSG Geodetic Parameter Dataset, which is a collection of definitions of coordinate reference systems and coordinate transformations for global, regional, national or local applications.
PROJ4
PROJ.4 is a computer code library for performing conversions between mapping projections. The library is based on work done at the United States Geological Survey, but is now an OSGeo (Open Source Geospatial Foundation) project.
Examples of datums, systems and conversions and transfers
Australian Height Datum (AHD)
On 5 May 1971, Geoscience Australia, on behalf of the National Mapping Council of Australia, carried out a simultaneous adjustment of 97 230 kilometres of two-way levelling. Mean sea level for 1966-1968 was assigned a value of 0.000m on the Australian Height Datum (AHD) at 30 tide gauges around the coast of the Australian continent. The datum surface is that which passes through mean sea level at the 30 tide gauges and at as specified at a few other critical junction points.
AUSGeoid09
AUSGeoid09 is a 1’ by 1’ (approximately 1.8 km) grid used to transfer heights between the ellipsoid (GDA94) and the Australian Height Datum (AHD). Unlike previous versions of AUSGeoid (‘93/’98), AUSGeoid09 provides users with the height offset between the ellipsoid and AHD as opposed to the ellipsoid and the geoid.
World Geodetic System
The World Geodetic System (WGS) is a standard for use in cartography, geodesy, and navigation including by GPS. It comprises a standard coordinate system for the Earth, a standard spheroidal reference surface (the datum or reference ellipsoid) for raw altitude data, and a gravitational equipotential surface (the geoid) that defines the nominal sea level.
The latest revision is WGS 84 (aka WGS 1984, EPSG:4326, G2139), established in 1984 and last revised in January 2021. Earlier schemes included WGS 72, WGS 66, and WGS 60.
WGS 84 is the reference coordinate system used by the Global Positioning System.
Geocentric Datum of Australia 1994
The Geocentric Datum of Australia (GDA2020) is the official geodetic datum adopted nationally across Australia on 1 January 2000. GDA2020 replaced the Australian Geodetic Datum 1994 (AGD94) as the GDA2020 coordinates are approximately 1.8 metres to the north east of GDA94 coordinates, which represents the tectonic motion of the Australian plate between 1994 and 2020. The standard map projection associated with GDA2020 is the Map Grid of Australia 2020 (MGA2020), a transverse Mercator projection that conforms to the internationally accepted Universal Transverse Mercator Grid system.
GDA2020 is a coordinate reference system that best fits the shape of the earth as a whole. It has an origin that coincides with the centre of mass of the earth, hence the term ‘geocentric’ GDA2020 is a static coordinate datum based on the International Terrestrial Reference Frame 2014 (ITRF2014), held at the reference epoch of 1 January 2020. Except for a small difference in the flattening term, the reference ellipsoid used with WGS84 is essentially the same as the Geodetic Reference System 1980 (GRS80) ellipsoid used with ITRF and hence GDA2020.
International Terrestrial Reference Frame & System
The Earth is constantly changing shape. To be understood in context, when the motion of the Earth's crust is observed, it must be referenced. A Terrestrial Reference frame provides a set of coordinates of points located on the Earth's surface. It can be used to measure plate tectonics, regional subsidence or loading and or used to represent the Earth when measuring its rotation in space. This rotation is measured with respect to a frame tied to stellar objects, called a celestial reference frame.
The International Terrestrial Reference System(ITRS) is a world spatial reference system co-rotating with the Earth in its diurnal motion in space.
NZ Geoid 2016
The New Zealand Quasigeoid 2016 (NZGeoid2016) can be used to convert GPS derived ellipsoidal heights to New Zealand Vertical Datum 2016 (NZVD2016) normal-orthometric heights that relate more closely to mean sea level and the local gravity field. NZGeoid2016 can also be used to transform heights to any of the 13 official local vertical datums used across New Zealand.
NZGeoid2016 models the difference between the GRS80 ellipsoid and the geoid over the New Zealand region. The geoid is a theoretical surface of equal gravity that roughly approximates the mean level of the sea across the Earth. NZGeoid2016 is published by LINZ and was computed by enhancing the EGM2008 global gravity model with terrestrial gravity observations over New Zealand and DNSC08 satellite altimetry data over the oceans. The model is published on a one arc-minute grid covering New Zealand's extended exclusive economic zone.
Summary
- A coordinate system is used to provide a reference system for determining positions and distances at a site.
- Coordinate systems are based on projections of the Earth. The shape of the Earth being approximated by spheres, ellipsoids and geoids.
- Different methods exist for 'unwrapping' projections of the Earth to form 2D maps. Projections of real 3D Earth views cause distortions on 2D maps.
- The coordinate system is based on a horizontal reference (Earth surface) and a vertical reference (height).
- Horizontal locations are generally specified in a grid of latitude and longitude, or Eastings and Northings.
- False Eastings and False Northings provide offsets from meridian and equatorial references to ensure positive distance values.
- Vertical heights are generally referenced to Mean Sea Level (MSL) or an Earth geoid.
- GPS uses an Earth ellipsoid as the vertical datum and needs a correction factor to calculate topological height (above MSL) or Geoid height.
- Many Datums and coordinate systems exist for international and or local use. It is important to understand their intended application.
- Conversions can be carried out between coordinate systems by considering the horizontal and vertical datums for each coordinate system.
- Note the time or date specifications. Time is an important consideration. Datums can originate at a particular time or over a particular duration. Using a different time basis could yield different datums. For example, sea levels vary constantly and require complicated analysis over time to determine an average. Earth surface (land mass) datums can also vary over time (years or decades) due to continental drift.