Geostatistical Modelling

Introduction

The objectives of ore-body modelling involve recognising that payable and unpayable zones may occur anywhere in an ore deposit. Suitable design of mining operations and the beneficial extraction of mineral resources necessitates a pre-knowledge of the tonnage and mean grade of blocks of ore in the deposit. Fulfilling this objective requires a sampling program, from which the results of chemical and physical analyses or of other important variables are recorded. Inferences about distributions and the amount and mean grade of reserves can only be drawn from this data.

The classical statistical approach assumes that the samples from which the unknown population is inferred are random samples , independent of each other. That is, taking one sample does not affect the outcome of the next.

The distribution of ore in a deposit is a geological phenomenon that is created, developed and controlled by complex geological processes, so that the similarity between two points in a deposit is really the degree of similarity of local geological environments, and points in a common environment reveal more similarity than those in different ones. As a result, geological samples are not randomly distributed and they are not independent of each other. There is an essential spatial relationship between geological samples that is lost in normal statistical definition and this implies that classical statistics are insufficient to describe an orebody fully.

There are some estimation methods that attempt to account for the spatial disposition of a block of ore and the samples, such as inverse distance weighting methods (Fig. 1). These assign weights to the samples that are inversely proportional to their distances from the panel being estimated. Hence samples nearer to the centre of the panel are given more weight than the more distant ones. Thus, spatial relationships are put on a very rough and empirical basis, with a lack of consideration towards the statistical characteristics of samples.

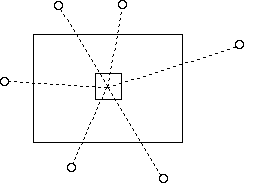
Figure 1 - Inverse Distance Method

Another method is the polygonal method (Fig. 2), in which an area of influence is defined for each drillhole and a weighted average grade is calculated on the assumption that the thickness or accumulation of the borehole in each polygon extends uniformly over the whole of the polygon; the weighting factor is the area of the polygon. A pronounced disadvantage of this method is that it promotes randomness, individual boreholes are evaluated independently and without searching for mutual relations and interdependence.

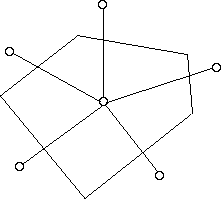
Figure 2 - Polygonal Method

With these conventional methods of modelling there is no way to calculate the error of estimations. The under-estimation of low grade blocks and the over-estimation of high grade blocks are other undesirable features that may arise from the use of these conventional methods.