Geostatistical Modelling
Proportional Effect and Relative Variograms
A fundamental assumption that is often made in geostatistical modelling techniques, is the assumption of stationarity or realisation of the intrinsic hypothesis. In other words the model variogram derived for a subset of the mineralisation can be used for the valuation of blocks of ore in the same or in a different section of the deposit. This in fact implies that the sample differences are only dependent on their relative distances not on their actual position.
There are situations in which these conditions are not satisfied and lack of stationarity is observed. In these circumstances an attempt has been made to justify the presence of stationarity for some limited neighbourhood, (that is, quasi-stationarity) which led to the development of universal Kriging . In practice, however, the lack of stationarity is often linked to the presence of a "Proportional Effect". This is, as the mean increases the variance of samples increases proportionally, or the semi-variograms vary as a function of the average value of the pairs.
To determine whether such a relationship exists, it is necessary to divide the deposit into areas of equal size, calculate a semi-variogram for each area and plot variographic parameters versus mean of assay values in each area. Or, since theoretically the sill value of a variogram is equivalent to the variance of samples, plots of mean assays of each area vs their standard deviations will suffice (Fig. 16).
Figure 16 - Relational Diagram between Mean and Standard Deviation
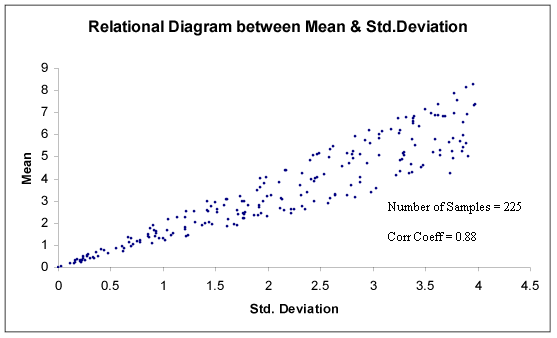
The presence of a proportional effect is always associated with log-normal behaviour, in which case assumption of the presence of proportional effect and the use of relative variograms avoids the transformation to log values and performance of log-normal Kriging .

