Geostatistical Modelling

Auxiliary Functions

Knowledge of variances or semi-variograms relating to samples or blocks which need not be of the same size, play a very important part in all practical applications of geostatistics.

It is often required for instance, to calculate the variance of blocks of a given size to forecast say variability of ore at stockpile. That is, variance of samples in the deposit minus the variance of samples in the block. The variance of samples in the deposit can be easily calculated by taking the statistical variance of samples. Conventional methods of numerical integration can be used, that is the block is divided into the smaller cells of equal size and the average variogram is obtained between all possible pairs of cells in the block.

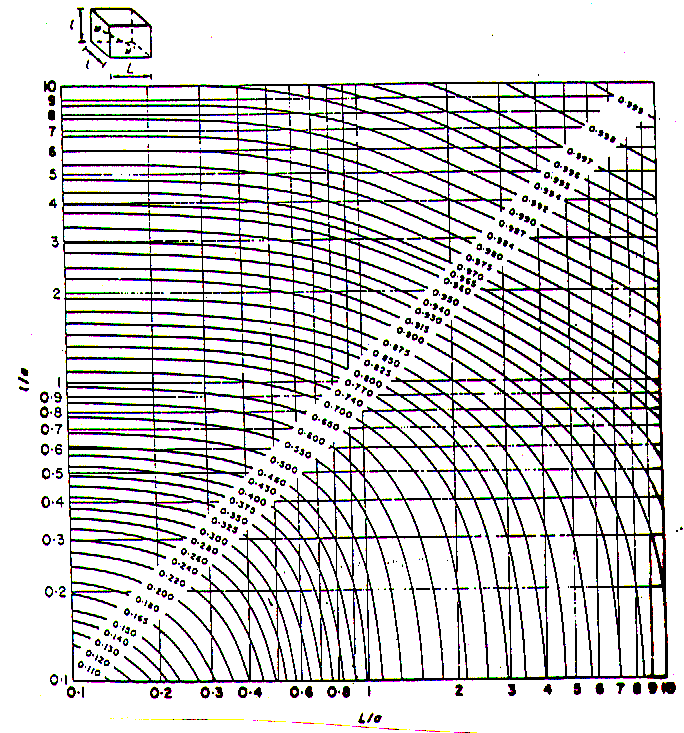
For ease, a series of functions (Auxiliary) have been developed to characterise the most commonly used value variance relationships (Fig. 17 - 21).

---

Figure 17 - Spherical Model - One Dimensional Auxiliary Function

---

Figure 18 - Spherical Model - Function X (L;l)

---

Figure 19 - Spherical Model - Function H(L;l)

---

Figure 20 - Spherical Model - Function F (L;l)

---

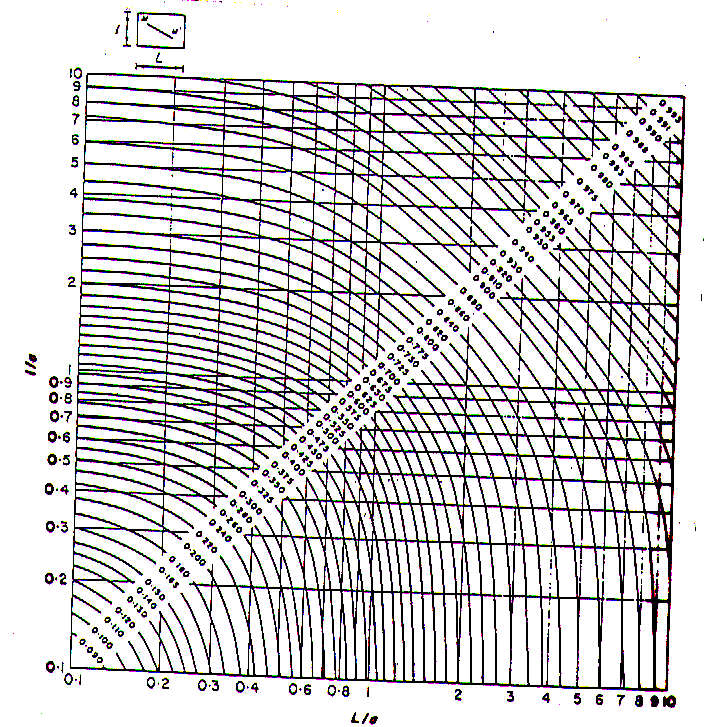
Figure 21 - Spherical Model - Function F(L;l2)