Variography parameters

Use this section of the interface to correct geometric (where grade variation in one direction is x times the variation in another direction) and zonal anisotropy (in deposits where mineralisation is layered or stratified). Correction for zonal anisotropy gives only positive results.

Read Variogram from file

Select this check box to use an existing variogram model. The drop-down list displays all .vrg files found in your current working directory. Click Browse to select a file from another location.

Nugget

Enter the nugget. This represents the random variability and is the value of the variogram at distance (h) ~ 0.

Variogram Parameters Selection

The variogram model type can be one of the following:

Spherical

This type is the most commonly used for ore deposits. They exhibit linear behaviour at and near the origin then rise rapidly and gradually curve off.

Exponential

This type is associated with an infinite range of influence.

The sill is reached at the specified range parameter. In release 3.2 and earlier, users were required to enter a range parameter of one-third the practical sill range. To use this model, enter the practical distance of the sill as a range parameter. For backward compatibility, see the Exponential Model 3.

Gaussian

This type exhibits parabolic behaviour at the origin and, like the spherical model, rises rapidly. The Gaussian type reaches its sill smoothly, which is different from the spherical model, which reaches the sill with a definite break. The Gaussian model is rarely used in mineral deposits of any kind. It is used most often for values that exhibit high continuity.

In release 3.2 and earlier, users were required to enter a sill range of 3 times the actual sill range. To use this model, enter the effective range of the sill. For backward compatibility, see the Gaussian model 3.

Linear

This type is a straight line with a slope angle defining the degree of continuity.

De-Wijsian

This type is a representation of a linear semi-variogram versus its logarithmic distance.

Power

This type is computed as M - d**p where M = the maximum correlation defined as 1000.0, d = distance from the origin, p = model power. For this model type only the power p is the major axis radius. Adjust the size of the ellipsoid so that the major axis is the desired power. The size of the ellipsoid for this model does not change the calculation of the variogram.

Exponential Model 3

This is an un-normalised exponential model for compatibility with release 3.2 and earlier. This variogram will have the practical sill at three times the distance entered as range parameter.

Periodic

This is a sine wave with one complete period over the effective range. This model is not commonly used because it can cause samples at greater distances to have higher correlation.

Gaussian Model 3

This is an un-normalised Gaussian model for compatibility with release 3.2 and earlier. The input radius must be the effective radius multiplied by 3.

Dampened Hole Effect

Dampening is achieved by multiplying the covariance function by an exponential covariance, that acts as a dampening function.

Refer to the Variogram Model Types section for a more detailed explanation of the mathematics related to variograms and diagrams of the variogram model types.

Sill Differential

Enter the sill differential. This represents the difference between the value of the variogram where it levels off and the nugget. For example, if you have a total sill of 1.0, and a nugget of 0.15, you want your sill differential to be 0.85 = (1.0 - 0.15).

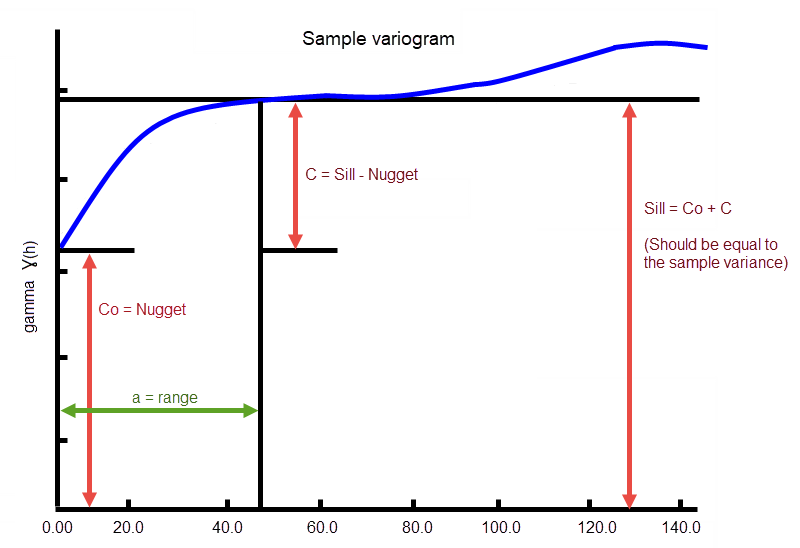
Figure 1: Sample Variogram

In the diagram, C₀is the nugget, and C is the sill differential.

Bearing/Plunge/Dip

Enter the bearing (Rotation about the Z axis), plunge (rotation about the Y axis) and dip (rotation about the X axis) of the variogram. Refer to Search Region for more information on bearing, plunge and dip.

Note: The terms bearing, plunge and dip have been used by various authors with various meanings. In this panel, as well as kriging, they do not refer to true geological bearing, plunge and dip.

Major/Semi-Major/Minor Axis radii

Enter the radii of the major, semi-major and minor axes of the variogram.