Matrix

Transform an Object by a Matrix

Use the Matrix option to use a matrix to transform an object. If you know the matrix you want to use, then you can specify it as part of this option. You can, however, use the Calculate option to create a matrix (either 2D or 3D) from a set of original and transformed points.

This option can also be accessed by selecting the Move by Matrix button from the Move toolbar. The Move toolbar is a "sub toolbar" and can either be accessed through the Modify toolbar or through using the Toolbar Visibility option (under the Tools menu).

---

Instructions

On the Design menu, point to Transformation, then click Matrix.

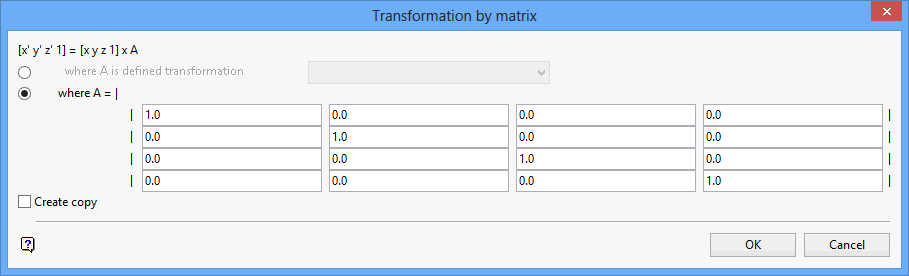
Transformation by matrix panel

where A is defined transformation

Select this option to use an existing transformation. The drop-down list contains all transformation parameters found in your Transformation Matrices file (<proj>.env_tran). The Transformation Matrices file should be located in your current working directory.

where A = I

Select this option to enter each element of the matrix. Keep in mind that transformation matrices entered through this panel are saved into the Transformation Matrices file. Refer to Appendix A for information on how to manually add matrices to this file

Create copy

Select this check box if you want the transformation to be applied to a copy of the object.

Select OK.

The Multiple Selection box is then displayed. Use the Multiple Selection box to choose your method of selecting the objects and select the objects.

If you are selecting by object, then the object will be transformed immediately. If you are selecting a category other than object, then the object that will be transformed is the first digitised object in the selected category and you will be asked whether or not you want to keep the change. If you do, then all other objects in the selected category will also be transformed.

Subsequent selections will have the same transformation applied unless you exit the option and re-select.

---

Advanced Information

Vulcan uses homogeneous coordinates to simplify the linear algebra required to carry out transformations (both forwards and backwards). These coordinates also make it possible to define to define perspective transformations.

Instead of representing a point in space as an X, Y and Z coordinate, that is (X, Y, Z), points are represented by an infinite number of four dimensional vectors, (W*x, W*y, W*z, W).

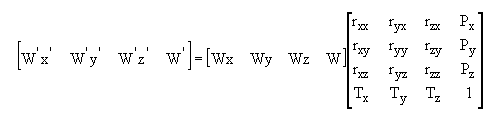
Figure 1 : The General Form of a Transformation Matrix

Perspective

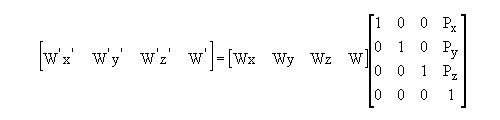
Figure 2 : The Matrix Transformation for Perspective Distortion

Where

P_x is the inverse of the X coordinate from where the image was viewed

P_y is the inverse of the Y coordinate from where the image was viewed

P_z is the inverse of the Z coordinate from where the image was viewed

Additional Information on Matrix Transformations

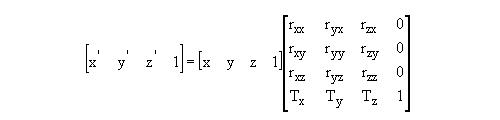
Figure 3 : Standard Form for a Transformation Matrix

If you want to perform a number of transformations, i.e. a rescale and a translation, then multiply the appropriate matrices together. For example, to rescale and then translate multiply the scaling and the translation matrices.

Translations

A translation is when an object is moved a given distance and direction. For example, transforming the point (1, 1, 1) to (2, 0, 4) and the point (2, 0, -2) to (3, -1, 1) is a translation.

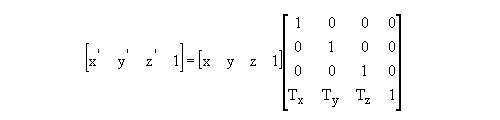
Figure 4 : The Matrix for Translations

Where

T_x is the X shift

T_y is the Y shift

T_z is the Z shift

In the above example, T_x = 1, T_y = -1, and T_z = 3.

Rescaling

Scaling is when an object is dilated or contracted.

Example:  Transforming the point (1, 1, 1) to (0.5, -1, 2) and the point (2, 0, -2) to (1, 0, -4) is a rescale.

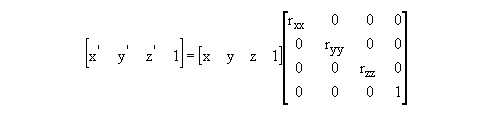
Figure 5 : The Matrix Transformation for Scaling along the Major Axes

Where

r_xx is the X scale factor

r_yy is the Y scale factor

r_zz is the Z scale factor

In the above example, r_xx = 0.5, r_yy = -1 and; r_zz = 2.

Rotation

Rotation in three dimensions requires the angle of rotation and an axis of rotation. The canonical rotations are defined when one of the positive X, Y or Z coordinate axes is chosen as the axis of rotation.

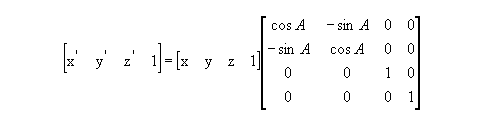
Figure 6 : Rotation about the Z-axis

Where

A is the angle of rotation about the Z-axis.

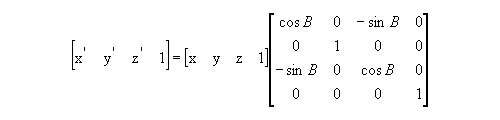
Figure 7 : Rotation about the Y-axis

Where

B is the angle of rotation about the Y-axis.

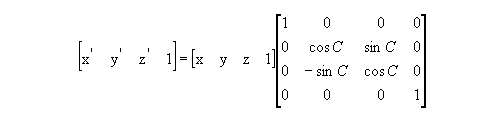
Figure 8 : Rotation about the X-axis

The general case of rotation about an Y-axis can be built up from these canonical rotations by using matrix multiplication.