Block Model
Use Block Model to specify a goal based on a block model variable, for example minimum cost, maximum grade, maximum metal, etc. For more information, see the Automatic Ramp Overview .
Instructions
The Automatic Ramp option uses a tree interface. Select branches from the tree menu on the left as described in the instructions below:
On the Underground menu, point to Development, and click Automatic Ramp, then select Block Model from the tree menu to display the Block Model panel.
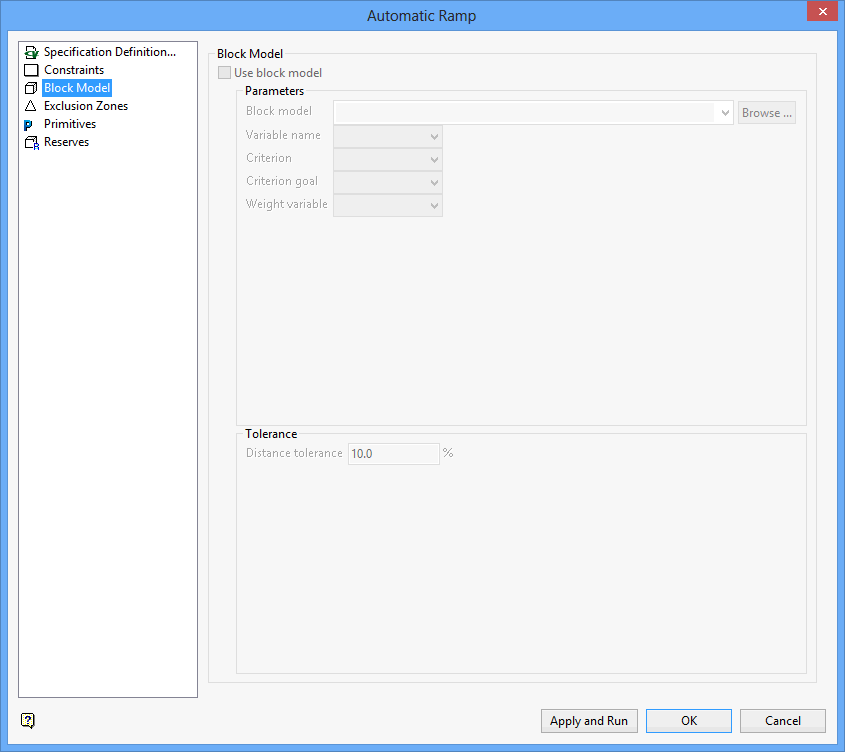
Block Model
Use block model
Select this check box to rank the ramps by the resulting block model variable. The ramps will be evaluated using this variable and the primitive shape (defined through the Primitives section).
Parameters
Block model
Select the block model that will be used to rank the ramps. The drop-down list contains all block models found in the current working directory. Click Browse to select a file from another location.
Variable name
Select the block model variable that will be used to evaluate the ramps.
Criterion
Spe cify the variable type ('Sum' or 'Average'). Use 'Sum' for cumulative values, for example mass, costs or profit, and 'Average' for grade type variables.
Criterion goal
Select 'Minimize' or 'Maximise'. The criterion goal selected depends on the nominated criterion variable. For example if a cost variable is used, then 'Minimize' will be the logical choice. If a grade or profit variable is used, then 'Maximize' is the preferred choi ce.
Weight variable
Specify the weighting variable, for example density. This field is only applicable when using the 'Average' criterion variable.
Tolerance
The tolerance value refers to how hard a feasible solution will be evaluated against the block model. For example, if you type '10' in the distance tolerance box, the algorithm will only evaluate the solutions that are within 10% of the distance of the current shortest solution.
So generally speaking, a small tolerance means fewer solutions are evaluated against the block model, conversely a higher value means more possible solutions are evaluated against the block model.
Related topics
Tutorial

